Wie Mathematik verständlich erklärt wird.
1. Gute Erklärungen sind vollständig und einfach
Die entscheidenden Eigenschaften einer guten Erklärung werden an dem folgenden bewusst kurz gehaltenen Beispiel verdeutlicht:
Aufgabe: Löse in dem Term 2 · (3x + 4) die Klammern auf !
2 · (3x + 4) = 2 · 3x + 2 · 4
a · ( b + c) = a · b + a · c
Man erkennt zunächst, dass die Aufgabe mit dem Distributivgesetz gelöst werden kann, weil eine Klammer mit einem Additionszeichen hier multipliziert wird.
Es sind a = 2 ; b = 3x und c = 4.
Die Formel des Distributivgesetzes gibt uns an,
wie wir vorgehen müssen.
Das a wird mit den beiden Teilen der Klammer verbunden.
Diese Erklärung hat 2 entscheidende Eigenschaften: Zunächst einmal ist sie vollständig. Alles, was der Schüler wissen muss, um diesen Sachverhalt zu verstehen, wird hier aufgeführt: Nichts Wichtiges fehlt. Die konkrete Aufgabe wird präzise mit dem abstrakteren Distributivgesetz verknüpft. Gerade Mathematiker, die sehr gut in ihrem Fach sind, neigen beim Erklären oft dazu, bestimmte Dinge wegzulassen, die für sie selbstverständlich sind.
Lehrerinnen und Lehrer müssen immer daran denken, dass für einen Schüler, der eine bestimmte Sache noch nicht verstanden hat, gar nichts selbstverständlich ist. Er muss wirklich alles erfahren, was im unmittelbaren Zusammenhang mit dem zu erklärenden Sachverhalt steht. Wenn man etwas Zentrales weglässt, dann ist es für den Schüler fast unmöglich, zu einem echten Verständnis zu gelangen.

Eine vollständige Erklärung zu finden ist nicht besonders schwierig. Denken Sie sorgfältig über den zu erklärenden Sachverhalt nach, dann werden sie auch alle Elemente ausfindig machen können, aus denen sich das Verständnis des Gegenstandes zusammensetzt.
Außerdem ist die obige Erklärung einfach. In klaren, nicht verschnörkelten Sätzen wird der Sachverhalt erläutert. Die Erklärung enthält nichts Überflüssiges, sie ist geradlinig und geht keine komplizierten Umwege, die das grundlegende Verständnis erschweren.

Oft tragen auch Beispiele dazu bei, eine Erklärung zu vereinfachen. Ausgebildete Mathematiker haben eine Fülle von Regeln im Kopf und sind durch ihr Studium besonders darin geschult, abstrakt zu denken. Man sollte nicht vergessen, dass Regeln nur dazu dienen, eine größere Anzahl von Einzelfällen im Gehirn zu einer Einheit zu verbinden.
Die Regel fasst unendlich viele Einzelfälle zusammen. Für einen Schüler stehen immer die Einzelfälle am Anfang des Verständnisses, und aus einer größeren Anzahl einzelner Beispiele kann dann später eine Regel gebildet werden. Aus diesem Grund sind Beispiele für viele Erklärungen äußerst nützlich, an manchen Stellen unverzichtbar.

Eine einfache Erklärung zu finden, ist gar nicht einfach. Man braucht oft Kreativität und Phantasie, um die einfachste Erklärung eines Sachverhaltes zu entdecken. Immer, wenn man denkt, dass die selbstgewählte Erklärung kompliziert ist, dann sollte man sich fragen, ob es nicht einen anderen Weg gibt, der dem Schüler einen leichteren Zugang zum Sachverhalt erlaubt. Das Ganze ist ein Prozess ständiger Verbesserung: Man sollte sich immer bemühen, zu noch einfacheren Erklärungen zu gelangen, um damit einer möglichst großen Anzahl von Schülern das Verständnis eines einzelnen mathematischen Zusammenhangs zu ermöglichen.

2. Der Begriff des kognitiven Netzes
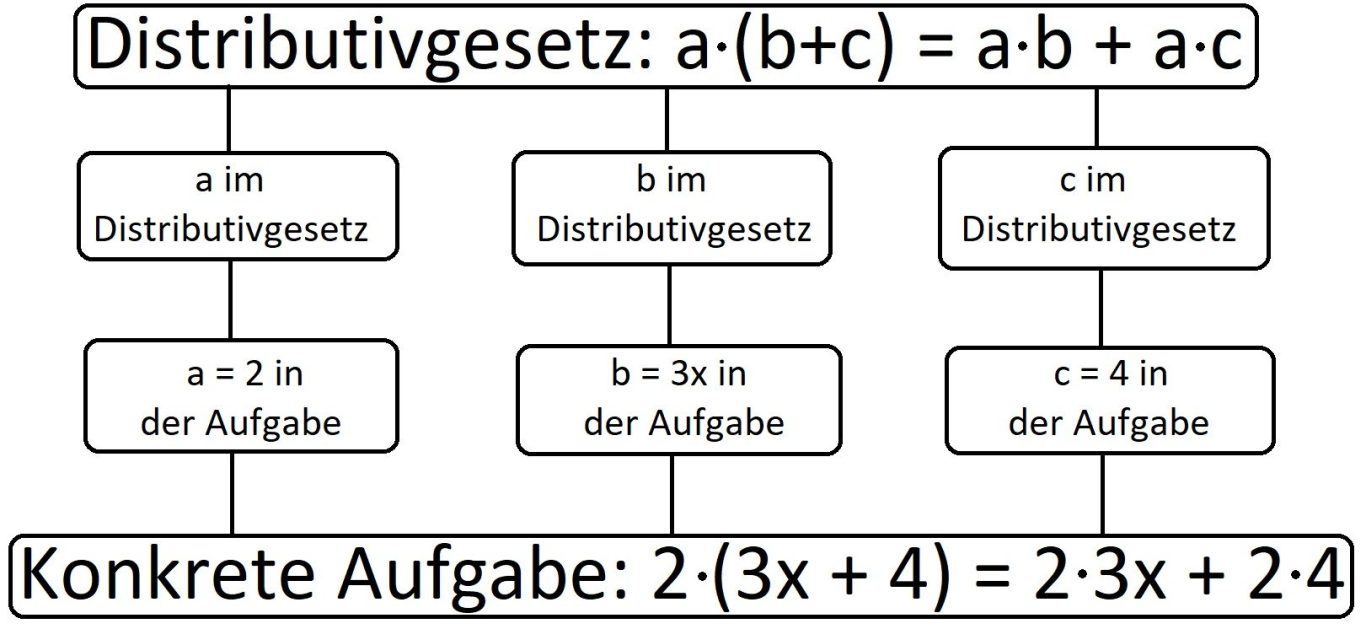
Wenn der Schüler dieses Beispiel wirklich verstanden hat, dann hat das in seinem Gehirn die in der obigen Grafik angegebene Form angenommen.
Aus nachvollziehbaren Gründen nenne ich dieses gesamte Gebilde ein kognitives Netz. Die 8 einzelnen Kästen bezeichne ich als Kognitionsknoten. Der Schüler hat den Sachverhalt verstanden, wenn er die 4 Kognitionsknoten des Distributivgesetzes mit den zugehörigen vier Kognitionsknoten der konkreten Aufgabe präzise verbinden kann.

Die Grafik ist ein exaktes Modell für die tatsächlichen Vorgänge im Gehirn. Man kann sich vorstellen, dass jeder einzelne der 8 Kognitionsknoten in einer Gruppe von Nervenzellen im Gehirn gespeichert ist. Falls der Schüler den Sachverhalt noch nicht verstanden hat, sind die Kognitionsknoten des Distributivgesetzes noch nicht mit den Kognitionsknoten der konkreten Aufgabe verbunden. Im Gehirn des Schülers sieht das so aus, dass die Nervenzellen des Distributivgesetzes noch keine Verbindung zu den Nervenzellen aufgenommen haben, in denen die konkrete Aufgabe gespeichert wurde.
Der Zweck der mathematischen Erklärung besteht nun darin, dass im Gehirn des Schülers eine Verbindung zwischen den Nervenzellen des Distributivgesetzes und den Nervenzellen der konkreten Aufgabe hergestellt wird. Die Verbindungslinien zwischen den Kognitionsknoten in der Grafik kann man sich ganz konkret als Nervenzellen vorstellen, die eine Verbindung zueinander aufgenommen haben. (Falls Sie mehr über die Funktionsweise des Gehirns wissen wollen, dann lesen sie „Das kleine Buch vom Gehirn“ von Prof. Dr. Michael Madeja, in dem das alles sehr anschaulich erklärt wird.)
Der Begriff des kognitiven Netzes ist ebenso fundamental wie allumfassend. Alles, was in unserem Gehirn gespeichert ist, kann durch dieses Modell dargestellt werden. In Ihrem Gehirn existiert zum Beispiel ein kognitives Netz zum Thema „Weihnachten“, das unter anderem die Kognitionsknoten „Bescherung“, „Weihnachtsbaum“ und „Christkind“ enthält.
Es geht also bei mathematischem Unterricht darum, kognitive Netze im Gehirn des Schülers zu bilden. Jetzt wird auch klar, warum die beiden Eigenschaften einer guten Erklärung so wichtig sind. Wenn eine Erklärung nicht vollständig ist, dann werden wichtige Kognitionsknoten einfach unterschlagen. Das Beispiel oben kann gar nicht verstanden werden, wenn man das Distributivgesetz nicht ganz konkret mit der Aufgabe verbindet. Wenn man das Distributivgesetz bei der Erklärung weglässt, dann entsteht kein echtes mathematisches Verständnis im Gehirn des Schülers, sondern etwas, das völlig zu recht als "Eselsbrücke" bezeichnet wird. Wie sollten unsere Schüler nicht wie Esel behandeln.

Aber auch die zweite Eigenschaft einer guten Erklärung ist wichtig. Wenn die Erklärung einfach ist, dann fällt es dem Schüler leichter, eine Verbindung zwischen den Kognitionsknoten aufzubauen. Spätestens jetzt ist klar, warum die beiden Kategorien "vollständig" und "einfach" so zentral sind.

3. Kognitive Netze in der Unterrichtspraxis
Beim Erklären sollten die folgenden drei Teilkonzepte beachtet werden:
1. Um ein tiefgreifendes mathematisches Verständnis bei den Schülern sicherzustellen, müssen alle an der Aufgabe beteiligten Gesetze exakt notiert und präzise mit dem konkreten Beispiel verknüpft werden. So wird die Erklärung vollständig. Im obigen Beispiel werden die Variablen a, b und c des Distributivgesetzes mit den entsprechenden Bestandteilen der Aufgabe verbunden. In der Praxis ist es entscheidend, etwa mit einem Stift im passenden Moment auf die Variablen der Formel und der Aufgabe zu zeigen. Es müssen grundsätzlich alle an der Aufgabe beteiligten Formeln und Gesetze aufgeschrieben und mit den konkreten Aufgaben verbunden werden, so dass das kognitive Netz vollständig ist.

Für eine vollständige Erklärung ist es auch sehr wichtig, dass man keine Zwischenschritte weglässt. Sobald Sie zum Beispiel bei der Lösung einer Gleichung einen Zwischenschritt weglassen, dann fehlt in der Erklärung eine ganze Zeile. Diese zusätzliche Zeile muss der Schüler nun in seinem Gehirn selbstständig erzeugen, ohne dass der Schüler die Zeile sieht. Die fehlende Zeile kann jetzt nicht mehr ausführlich erklärt werden. Vor allem leistungsschwächere Schüler werden so vor große Schwierigkeiten gestellt. Wenn sie Frust bei ihren Schülern vermeiden wollen, dann lassen Sie grundsätzlich keine Zwischenschritte weg !

2. Damit die Erklärung so einfach wie möglich wird, achten Sie vor allem auf ihre Sprache. Man sollte es möglichst vermeiden, komplizierte, verschachtelte Satzkonstruktionen zu benutzen, wenn man etwas erklärt. Sprechen Sie in kurzen Sätzen, verwenden Sie möglichst einfache Worte. Achten Sie auch darauf, langsam zu reden, so dass die Schüler auch genug Zeit haben, die Aufgabe tatsächlich zu verstehen.
Denken Sie im Vorfeld auch gründlich über die didaktische Aufbereitung der Aufgaben nach: Das Ziel ist es, dass die Erklärung so einfach wie möglich wird. Oft ist es so, dass es mehrere Erklärungswege für die Aufgabe gibt, dann ist es Ihre Aufgabe, den leichtesten zu finden.

3. Was machen Sie, wenn die Schüler die Erklärung nicht sofort verstehen ? Nehmen wir an, sie haben einen bestimmten Sachverhalt ein einziges Mal erklärt, und der Schüler hat es noch nicht begriffen. Beim Schüler entsteht im Gehirn gerade ein kognitives Netz, das zu diesem Zeitpunkt vielleicht so aussieht wie in der Abbildung hier:
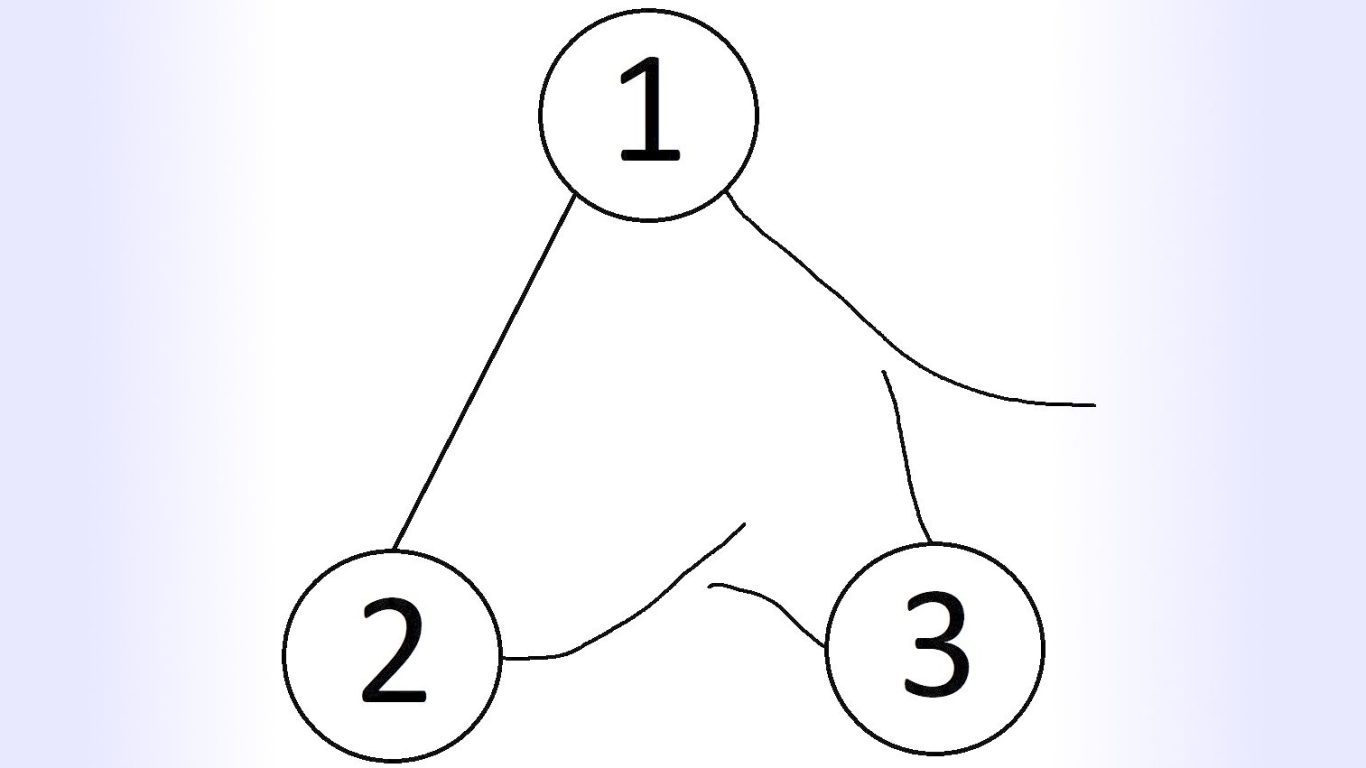
Die Kognitionsknoten 1 und 2 wurden bereits präzise verbunden, der Knoten 3 ist auch schon im Gehirn gespeichert, aber der Schüler hat noch nicht verstanden, was der Kognitionsknoten 3 mit den beiden anderen Knoten zu tun hat. Das Gehirn des Schülers versucht gerade, eine Verbindung vom Knoten 3 zu den beiden anderen Knoten herzustellen. Wie sorgen wir dafür, dass das auch klappt ?
Viele Lehrer neigen dazu, es jetzt mit einer neuen Erklärung zu versuchen, frei nach dem Motto: "Durch die erste Erklärung hat der Schüler es nicht verstanden, also probiere ich etwas Neues." Das ist völlig falsch, und zwar aus folgendem Grund: Wie man an der Skizze oben sehen kann, hat die erste Erklärung bereits Spuren im Gehirn des Schülers hinterlassen: Das kognitive Netz entsteht gerade. Wird der Schüler jetzt mit einer neuen Erklärung konfrontiert, dann beginnt der Konstruktionsprozess des kognitiven Netzes von vorn. Dem Schüler ist zu Beginn gar nicht klar, was die zweite Erklärung mit der ersten zu tun hat. Stattdessen sollte man die erste Erklärung nun möglichst wortgetreu wiederholen. Dadurch kann das Gehirn seine Arbeit fortsetzen, und mit etwas Glück gelingt es nun, das Bild oben in ein vollständiges kognitives Netz zu verwandeln. Normalerweise macht es spätestens beim dritten Durchgang mit der selben Erklärung "klick", und der Schüler hat es verstanden.

Diese Theorie mit den Kognitionsknoten habe ich am Anfang der Nullerjahre erdacht. Seitdem habe ich sie hunderte Male im Unterricht konkret angewendet. Durch eine möglichst exakte Wiederholung der Erklärung kommt es tatsächlich zu einem spürbaren Erkenntnisgewinn bei den Schülern. Es hilft wirklich, eine Erklärung wortgetreu zu wiederholen ! Die Praxis lügt nicht.
Die folgende Grafik fasst die entscheidenden Regeln für sinnvolle Erklärungen im Mathematikunterricht zusammen:

4. Warum gute Erklärungen so wichtig sind
Das Fach Mathematik kann starke Emotionen in den Lerngruppen auslösen, die allein davon abhängen, ob man die Inhalte versteht oder nicht. Falls Schüler Mathematik im Unterricht nicht verstehen, dann entsteht in sehr vielen Fällen eine äußerst unangenehme Mischung aus Scham und Angst. Man fühlt sich dumm, wenn man es nicht versteht, und dieses Gefühl findet jeder Mensch äußerst unangenehm. Und dazu kommt dann noch die Angst, dass der Lehrer und die Mitschüler bemerken könnten, dass man die aktuellen Aufgaben nicht lösen kann.
Es ist kein Zufall, dass kein anderes Schulfach so negative Emotionen auslöst wie Mathematik. Wenn man in diesem Fach nicht gut ist, dann ist das viel unangenehmer, als wenn man in Englisch oder Deutsch Probleme hat, was auch daran liegt, dass man in Mathematik Verständnislücken nicht durch fleißiges Lernen ausgleichen kann. Falls man es nicht versteht, dann kann man so fleißig sein wie man will, es wird nichts nützen: Das ist in keinem anderen Fach so extrem wie in der Mathematik. Deswegen ist dieses Fach für manche Schüler psychisch sehr belastend.

Falls man die Inhalte jedoch versteht, entstehen ganz andere Gefühle. Es macht kaum etwas in der Schule so viel Spaß wie die erfolgreiche Lösung einer mathematischen Aufgabe. Das liegt daran, dass beim zielgerichteten Rechnen das Hormon Dopamin im Körper ausgeschüttet wird. Falls man Mathe versteht, entsteht ein echtes Glücksgefühl ! Die Schüler fühlen sich schlau, und das ist ein schönes Gefühl !

Es ist fast ausschließlich von der Qualität der Erklärungen der Mathematiklehrerin abhängig, ob die Lerngruppen Freude an Mathematik entwickeln oder im Gegensatz dazu Angst und Scham mit diesem Fach verbinden. In der heutigen Lehrerausbildung wird sehr viel Wert darauf gelegt, dass Schülerinnen und Schüler möglichst selbstständig arbeiten.
Natürlich ist es sehr wichtig, dass die Lerngruppen im Mathematikunterricht selbstständig Aufgaben lösen. In der Schule geht es grundsätzlich darum, die intellektuellen Fähigkeiten der Schüler zu fördern, und das funktioniert nur, wenn die Schüler selbst über Mathematik nachdenken. Doch wie gelingt dieses selbstständige Nachdenken ?
Schüler können nur dann eigenständig eine Aufgabe lösen, wenn sie genau verstanden haben, worum es geht. Die präzisen Erklärungen sind unverzichtbar, um die Schüler in die Lage zu versetzen, selbst mathematische Problemstellungen zu lösen.

Aus diesem Grund gibt es in einem sinnvollen Mathematikunterricht einen stetigen Wechsel zwischen zwei Unterrichtsformen: Phasen mit präzisen Erklärungen im Unterrichtsgespräch wechseln sich ab mit Zeiten, in denen die Lerngruppe ohne die Hilfe der Lehrerin rechnet. Erst durch die verständlichen Erklärungen des Lehrers wird das selbstständige Nachdenken der Schüler über Mathematik ermöglicht, und durch diese Vorgehensweise werden die Klassen dann auch immer kompetenter beim Lösen der Aufgaben. So entsteht bei den Schülern Freude an Mathematik.

© Volker Klugmann 2023. Alle Rechte vorbehalten.
Wir benötigen Ihre Zustimmung zum Laden der Übersetzungen
Wir nutzen einen Drittanbieter-Service, um den Inhalt der Website zu übersetzen, der möglicherweise Daten über Ihre Aktivitäten sammelt. Bitte überprüfen Sie die Details in der Datenschutzerklärung und akzeptieren Sie den Dienst, um die Übersetzungen zu sehen.